Análisis de sentimientos en tweets relacionados con el #ChaTeo y el equipo tiburón.

En esta ocasión quiero compartirles un trabajo que he realizado basado en algo que anteriormente desarrollé cuando estaba en mi primera temporada en la cancha de Boca. Se trata de la recolección en tiempo real de tweets relacionados con el #chateo y mi amado equipo tiburón, seguido de un análisis de sentimientos a nivel sintáctico del texto de los mismos.

En ese primer trabajo que realicé en UniAndes, se necesitaba entre otros requerimientos lograr un análisis de polaridad que clasificara los tweets del cachonismo electoral que era tendencia por esos días empleando al menos un modelo básico de 3 categorías: positivo, neutro y negativo. Sin embargo mi inquietud y espíritu de investigación me llevó a un trabajo expuesto por miembros de la Universidad del estado de Carolina del Norte, que empleaba un modelo de 2 dimensiones para describir el sentimiento de un tweet o texto corto cualquiera. 

En ese trabajo se proponía emplear el modelo de Russell que permite clasificar el afecto emocional en un plano bidimensional, considerando como dimensiones la valencia (que varía desde lo negativo a lo positivo) y un nivel de excitación o agitación (que va de bajo a alto). El modelo en mención es ilustrado en la siguiente figura:

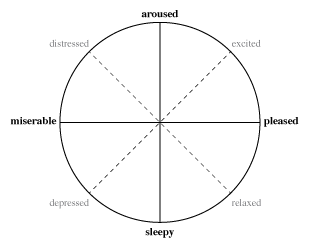
El proyecto citado también describía el procedimiento y modelo matemático para lograr establecer una medida que permitiera totalizar y ponderar todo el contenido del tweet, transformándolo en una pareja ordenada que se pudiera ubicar en el plano anterior.

En primera instancia es importante anotar que el trabajo citado utiliza un diccionario extendido (ANEW: Affective Norms For English Words) de palabras en inglés anotadas por varios grupos de investigadores especialistas en el área del fashion psicológico de universidades de USA, proporcionando medidas de valencia y agitación ---con medidas estadísticas relevantes para el modelo--- de varias decenas de miles de palabras en inglés. Como es natural comprender, los tweets objetivos de mi proyecto estarían escritos en español en su totalidad, por lo que rapidamente con ayuda de un servicio Web de traducción obtuve una primera versión factible para mi trabajo.

Cada palabra del diccionario construido tiene asignada una valencia y agitación, ambas descritas estadísticamente en términos de una media y desviación estandar asociada. Así por ejemplo, una de mis palabras favoritas "talento" se describe de la siguiente manera: 

talento: \( (v_{\mu} = 6.3, v_{\sigma}= 1.96) \) y \((a_{\mu} = 5.6, a_{\sigma}= 1.93)\)

El proceso para establecer una media global para la valencia y agitación de todo un tweet se presenta a continuación:

1. Se referencia cada palabra \(w_i\) del diccionario que se encuentre en el texto del tweet.
2. Sí un tweet contiene menos de dos palabras del diccionario, se descarta este tweet debido que  se considera que no se puede dar una estimación confiable del sentimiento.
3. Se calculan la media global de la valencia \(M_v\) y la media global de la agitación \(M_a\) de todo el tweet promediando estadísticamente las \(n\) medias de la valencia y agitación de las palabras.

Es evidente que no se deben calcular las medias globales ponderando uniformemente las medias de las variables de interés respectivamente, por ello asumiendo que las medidas del diccionario fueron generadas siguiendo una distribución normal, se utiliza la función de densidad de probabilidad de una distribución normal para calcular los pesos asociados a cada palabra a la hora de estimar la media global de la valencia y agitación de todo el tweet. El cálculo de estos pesos corresponde a la probabilidad que el valor de la variable de la fdp sea exactamente la media. A continuación se presentan las expresiones respectivas:

\[M_v=\frac{\sum_{i=1}^{n} v_{\mu_i} N(v_{\mu_i}, v_{\mu_i}, v_{\sigma_i})}{\sum_{i=1}^{n} N(v_{\mu_i}, v_{\mu_i}, v_{\sigma_i})}\]

\[M_a=\frac{\sum_{i=1}^{n} a_{\mu_i} N(a_{\mu_i}, a_{\mu_i}, a_{\sigma_i})}{\sum_{i=1}^{n} N(a_{\mu_i}, a_{\mu_i}, a_{\sigma_i})}\]

Para los que no recuerdan la fdp de una distribución normal aquí se las presento nuevamente. No es sólo por meterles los monos, puesto que para muchos programadores esto sólo se reduce a importar alguna librería y rapidamente ya la pueden evaluar:

\[N(x, \mu, \sigma)=\frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

Bueno ahora sí, como dicen los vendedores ambulantes en los buses, sin mas cuentos ni más chistes les presentó la solución Web donde se visualizan los resultados obtenidos. Con algo de ingeniería inversa me tumbé el componente de visualización que encontré en el sitio del proyecto que propuso el modelo. Estas son algunas capturas de los tweets recolectados y clasificados segun el modelo previamente presentado.

Los tweets fueron recolectados usando la API de Twitter en tiempo real durante los días en los cuales al equipo tiburón le tocaba wapear contra el "Flamingo" y el equipo "Abérica de Cali", siendo este último el club del alma del cacha que vive en un arenero también llamado Valle del cacique Upar.

Estos son algunos tweets clasificados positivamente según el modelo:

Ahora es el turno de un par de tweets negativos:

Y para cerrar una aglomeración de tweets jocosos y cayamanadas, jejejejje: